本文将主要涵盖以下内容:
- 从理论角度推导 Muon 优化器,介绍其「控制谱范数下的最速下降」的特性,主要在 Bernstein 的博客 https://jeremybernste.in/writing/deriving-muon 的基础上进行延伸。值得注意的是,推导的过程跟真正实现上有差异,比如实际是对动量进行正交化,而不是对梯度,但读者无须担心,本文最后还是会回归到具体的实现
- 介绍 Kimi 团队 https://github.com/MoonshotAI/Moonlight 在 Muon 基础上的改进和代码实现,主要是 weight decay 以及对齐更新量的 RMSNorm 两个方面
- 逐一实现上面提及的 Muon,然后与原始的 Adam 做对照实验进行验证
- 最后对 Muon 进行 FLOPS 分析
推导 Muon
度量线性层
给定输入 $\boldsymbol{x} \in\mathbb{R}^{n}$,权重矩阵 $\mathbf{W}\in\mathbb{R}^{m \times n}$,过一层「线性层」(Linear Layers),即 $\boldsymbol{y} = \mathbf{W}\boldsymbol{x}$(这里对 bias 进行忽略)。那么有个有趣的问题,$\mathbf{W}$ 究竟对输入做了什么?或者如何度量这种线性运算呢?
此时可以联系一下「算子范数」(Operator Norm)的定义:给定任意两种 norm 方式 $\| \cdot\|_{\text{F}}$ 和 $\|\cdot\|_{\text{E}}$,对于任意的 $\boldsymbol{x}$,算子范数是 $\mathbf{W}$ 能对 $\boldsymbol{x}$ 进行的最大拉伸量:
$$ \|\mathbf{W}\|_{\text{op}} := \max_{\boldsymbol{x}\neq \boldsymbol{0}} \frac{\|\mathbf{W}\boldsymbol{x}\|_{\text{F}}}{\|\boldsymbol{x}\|_{\text{E}}} $$
接着让我们看看两种 norm 方式 $\|\cdot\|_{\text{F}}, \|\cdot\|_{\text{E}}$ 均为 RMSNorm 时会发生什么,先回顾下 RMSNorm 的定义:
$$ \|\boldsymbol{x}\|_{\text{RMS}} = \sqrt{ \frac{1}{n} \sum_{i} \boldsymbol{x}_{i}^{2}} = \sqrt{ \frac{1}{n} } \|\boldsymbol{x}\|_{2} $$
那么:
$$ \|\mathbf{W}\|_{\text{RMS} \to \text{RMS}} := \max_{\boldsymbol{x} \neq \boldsymbol{0}} \frac{\|\mathbf{W}\boldsymbol{x}\|_{\text{RMS}}}{ \|\boldsymbol{x}\|_{\text{RMS}}} = \sqrt{ \frac{n}{m} }\underbrace{ {\color{#08F} \max_{\boldsymbol{x} \neq \boldsymbol{0}} \frac{\|\mathbf{W}\boldsymbol{x}\|_{2}}{\|\boldsymbol{x}\|_{2}}} }_{\text{L2 operator norm} } \tag{\#1} $$
可以发现 RMSNorm 算子范数是一种归一化后的 L2 算子范数,那么 L2 算子范数究竟是什么呢?我们接着推导:
首先对 $\mathbf{W}$ 进行「奇异值分解」(SVD),即 $\mathbf{W}=\mathbf{U\Sigma V^{\top}}$,其中 $\mathbf{U}, \mathbf{V}$ 都是正交矩阵,而 $\mathbf{\Sigma}$ 是对角矩阵,对角线的元素为奇异值,不妨设 $\sigma_{1}\geq\sigma_{2}\geq \dots \geq\sigma_{r}, \, r=\min(m,n)$
先说明一个重要的性质,即「正交变换之后不改变 L2 范数的大小」,证明如下:因为 $\mathbf{V}$ 是正交矩阵,所以 $\mathbf{V}^{\top}\mathbf{V} = \mathbf{I}_{n}$
$$ \|\mathbf{V}\boldsymbol{x}\|_{2}^{2} = (\mathbf{V}\boldsymbol{x})^{\top}\mathbf{V}\boldsymbol{x} = \boldsymbol{x}^{\top}\underbrace{ \mathbf{V}^{\top}\mathbf{V} }_{ \mathbf{I}_{n} }\boldsymbol{x} = \boldsymbol{x}^{\top}\boldsymbol{x} = \|\boldsymbol{x}\|_{2}^{2} $$
接着开始正式推导 L2 算子范数,不妨记 $\mathbf{V}^{\top}\boldsymbol{x} = \boldsymbol{y}$,蓝色部分的变换都用到了刚刚提及的「正交变换之后不改变 L2 范数的大小」的性质
$$ \frac{\|\mathbf{W}\boldsymbol{x}\|_{2}}{\|\boldsymbol{x}\|_{2}} = \frac{\|\mathbf{U\Sigma V^{\top}}\boldsymbol{x}\|_{2}}{\|\boldsymbol{x}\|_{2}} = \frac{\|\mathbf{U\Sigma}\boldsymbol{y}\|_{2}}{{\color{#08F}\|\boldsymbol{y}\|_{2}}} = \frac{{\color{#08F}\|\Sigma \boldsymbol{y}\|_{2}}}{\|\boldsymbol{y}\|_{2}} $$
那么:
$$ \max_{\boldsymbol{x}\neq \boldsymbol{0}} \frac{\|\mathbf{W}\boldsymbol{x}\|_{2}}{\|\boldsymbol{x}\|_{2}} \implies \max \frac{\|\Sigma \boldsymbol{y}\|_{2}^{2}}{\|\boldsymbol{y}\|_{2}^{2}}= \frac{\sum_{i}\sigma_{i}^{2}y_{i}^{2}}{\sum_{i}y_{i}^{2}}\leq \frac{\sigma_{1}^{2}\sum_{i}y_{i}^{2}}{\sum_{i}y_{i}^{2}} = \sigma_{1}^{2} $$
即:
$$ \max_{\boldsymbol{x} \neq \boldsymbol{0}} \frac{\|\mathbf{W}\boldsymbol{x}\|_{2}}{\|\boldsymbol{x}\|_{2}} = \sigma_{1} = \sigma_{\text{max}} = \underbrace{ \|\mathbf{W}\|_{2} }_{ \text{Spectral Norm} } $$
「谱范数」(Spectral Norm)指的是矩阵的最大奇异值,那么联系式 $\#1$ 可得:
$$ \|\mathbf{W}\|_{\text{RMS} \to \text{RMS}} = \sqrt{ \frac{n}{m} }{ \max_{\boldsymbol{x} \neq \boldsymbol{0}} \frac{\|\mathbf{W}\boldsymbol{x}\|_{2}}{\|\boldsymbol{x}\|_{2}}} = \sqrt{ \frac{n}{m} }\|\mathbf{W}\|_{2} \tag{\#2} $$
RMSNorm 的算子范数是一种归一化的谱范数
输出变化量
在训练神经网络时,我们想知道,当权重矩阵更新后,输出会多大程度随之变化(当然这里 $\boldsymbol{x}$ 也会发生变化,会在后文论述),即:
$$ \Delta \boldsymbol{y} = (\mathbf{W}+\Delta \mathbf{W})\boldsymbol{x} - \mathbf{W}\boldsymbol{x} = \Delta \mathbf{W}\boldsymbol{x} $$
联系式 $\#1$ 的定义,可知:
$$ \|\Delta \boldsymbol{y}\|_{\text{RMS}} = \|\Delta \mathbf{W}\boldsymbol{x}\|_{\text{RMS}} \leq \|\Delta \mathbf{W}\|_{\text{RMS}\to \text{RMS}} \cdot\|\boldsymbol{x}\|_{\text{RMS}} \tag{\#3} $$
换言之,当权重矩阵更新后,我们找到了输出变化量 RMSNorm 的最大值,这里利用算子范数,巧妙地将矩阵的更新和输出的更新联系了起来
对偶化梯度
通过「泰勒展开式」(Taylor Expansion),可知:
$$ \mathcal{L}(\mathbf{W} + \Delta \mathbf{W}) = \mathcal{L}(\mathbf{W})+ \langle \nabla_{\mathbf{W}} \mathcal{L}, \Delta \mathbf{W} \rangle + \text{High Order Terms} $$
由于变化量比较小,不妨对高次项进行省略,即「线性近似」:
$$ \Delta \mathcal{L} = \mathcal{L}(\mathbf{W}+\Delta \mathbf{W}) - \mathcal{L}(\mathbf{W}) \approx \langle\nabla_{\mathbf{W}}\mathcal{L}, \Delta \mathbf{W}\rangle $$
我们肯定想要 loss 变化量越小越好,同时变化的过程中,我们并不希望输出变化量太大,否则就会破坏前面泰勒展开的前提;同时如果输出变化量太大,会让训练过程不稳定。那么我们就对输出变化量加个 bound,即:
$$ \min \, \langle \nabla_{\mathbf{W}}\mathcal{L},\Delta \mathbf{W}\rangle, \|\Delta \boldsymbol{y}\|_{\text{RMS}} =\mathcal{O}(1) $$
笔者以为「对输出变化量进行约束」即为 Muon 的核心 motivation,将式 $\#3$ 代入,则:
$$ \min \, \langle \nabla_{\mathbf{W}}\mathcal{L},\Delta \mathbf{W}\rangle, \, \|\Delta \mathbf{W}\|_{\text{RMS}\to \text{RMS}} \cdot\|\boldsymbol{x}\|_{\text{RMS}} =\mathcal{O}(1) $$
假设 $\|\boldsymbol{x}\|_{\text{RMS}} = \mathcal{O}(1)$,则:
$$ \min \, \langle \nabla_{\mathbf{W}}\mathcal{L},\Delta \mathbf{W}\rangle, \, \|\Delta \mathbf{W}\|_{\text{RMS}\to \text{RMS}} =\mathcal{O}(1) \tag{\#4} $$
式 $\#4$ 即被称为「对偶化梯度」(Dualizing the Gradients),那么这个如何解?
可以先展开一下约束,使其与谱范数联系起来:
$$ \begin{align} \|\Delta \mathbf{W}\|_{\text{RMS}\to \text{RMS}} = \sqrt{ \frac{n}{m} } \|\Delta\mathbf{W}\|_{2} =\mathcal{O}(1) \\ \implies \|\Delta\mathbf{W}\|_{2} =\mathcal{O}\left(\sqrt{\frac{m}{n}}\right) \end{align} $$
求解约束
接着我们对梯度进行奇异值分解: $\nabla_{\mathbf{W}}\mathcal{L}=\mathbf{U\Sigma V^{\top}}$,这里是「经济型分解」,即 $\mathbf{U}\in\mathbb{R}^{m\times r}, \mathbf{V}\in\mathbb{R}^{n\times r}, \mathbf{\Sigma} \in\mathbb{R}^{r \times r}$,其中 $r=\text{rank}(\nabla_{\mathbf{W}}\mathcal{L})\leq \min(m, n)$。假设没有约束的情况下,我们想要去 $\min \langle \nabla_{\mathbf{W}}\mathcal{L}, \Delta \mathbf{W}\rangle$,我们会直接按照梯度的反方向,即
$$ \Delta \mathbf{W} = - \nabla_{\mathbf{W}}\mathcal{L} $$
但目前有个约束条件,我们可以对 $\Delta \mathbf{W}$ 进行「正交化」(Orthogonalization), $c \in\mathbb{R}$ 是一个系数:
$$ \Delta \mathbf{W} = -c \cdot\mathbf{UV}^{\top} $$
之所以写成上述形式,主要是因为约束是有关谱范数的,而 $\|\mathbf{UV^{\top}}\|_{2}=1$,下面来证明这一性质。首先,对于一个矩阵 $\mathbf{A} \in \mathbb{R}^{m \times n}$ 来说,要求其谱范数,按照如下流程:
$$ \|\mathbf{A}\|_{2} = \sqrt{ \lambda_{\max}(\mathbf{A^{\ast}}\mathbf{A}) } = \sigma_{\max}(\mathbf{A}) $$
其中 $\mathbf{A}^{*}$ 是矩阵 $\mathbf{A}$ 的「共轭转置」(Conjugate Transpose),对于「实数域」的矩阵来说,共轭等于其自身,故而 $\mathbf{A}^{*}= \mathbf{A}^{\top}$,所以就可以求 $\|\mathbf{UV}^{\top}\|_{2}$
$$ (\mathbf{UV}^{\top})^{\top}\mathbf{UV^{\top}} = \mathbf{VU}^{\top}\mathbf{UV^{\top}} = \mathbf{VV^{\top}} = \mathbf{I}_{r}\implies \|\mathbf{UV}^{\top}\|_{2} = \sqrt{ \lambda_{\max} } = 1 $$
接着来计算一下权重更新量的谱范数:
$$ \|\Delta\mathbf{W}\|_{2} = \|-c\cdot \mathbf{UV^{\top}}\|_{2} = |c| \cdot \|\mathbf{UV^{\top}}\|_{2} = |c| $$
那么:
$$ \|\Delta \mathbf{W\|_{2}}=\mathcal{O} \left(\sqrt{ \frac{m}{n} } \right)\implies c =\mathcal{O}\left(\sqrt{ \frac{m}{n} }\right) $$
可得:
$$ \Delta \mathbf{W} = - \mathcal{O}\left(\sqrt{ \frac{m}{n} } \right)\mathbf{UV^{\top}} \tag{\#5} $$
即式 $\#5$ 就是对偶化梯度的解,小结一下,我们将对输出变化量的约束转为对权重变化量的谱范数要求,最后通过「正交化」来求解
求正交化
那么如何求正交化呢?正交化即让「奇异值全变为 $1$」,而奇异值是正数,就相当于对其使用了 sign 函数
$$ \nabla_{\mathbf{W}}\mathcal{L} = \mathbf{U\Sigma V^{\top}} \mapsto \mathbf{UV^{\top}} $$
但是要分解完 SVD,再对 $\Sigma$ 使用 sign,这个代价有点大,有没有直接在 $\nabla_{\mathbf{W}}\mathcal{L}$ 上作用的办法呢?有一条推论可以借助:「奇次矩阵多项式(Odd Matrix Polynomials)和 SVD 存在可交换性」,即我们对 $\nabla_{\mathbf{W}}\mathcal{L}$ 的操作等于对 $\Sigma$ 进行操作:
$$ p(\nabla_{\mathbf{W}}\mathcal{L}) = p(\mathbf{U\Sigma V^{\top}}) = \mathbf{U}p(\Sigma)\mathbf{V^{\top}} $$
但问题是 sign 并非是矩阵多项式的形式,奇次矩阵多项式一般长这样:
$$ p(\mathbf{X}):= a\cdot \mathbf{X} + b \cdot \mathbf{XX^{\top}X} + c\cdot \mathbf{XX^{\top}XX^{\top}X} + \dots $$
此时,就可以用一种 sign 近似 https://epubs.siam.org/doi/10.1137/0707031 来完成,即:
$$ p(\Sigma) := \frac{3}{2}\Sigma - \frac{1}{2}\Sigma\Sigma^{\top}\Sigma $$
可以用单变量来可视化看一下:
$$ p(x) = \frac{3}{2} x - \frac{1}{2} x^{3}; \quad p_{n}(x)= \underbrace{ p \circ p \circ \dots \circ p }_{ n }(x) $$
当 $n=14$ 时,可以发现,在 $[0, \sqrt{ 3 }]$ 范围内可以做到很好地近似 sign,即结果为 $1$
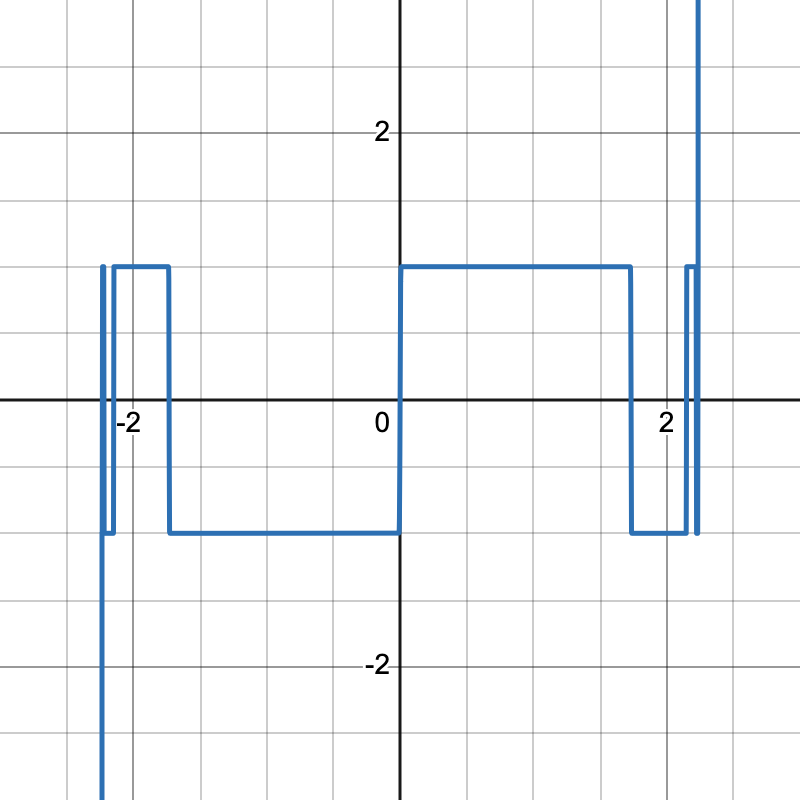
而上述过程被称为「Newton-Schulz Iteration」,因为我们的目的是想让 $\mathbf{\Sigma}$ 变成单位矩阵,所以也可称为矩阵的「零次幂」(Zero Power)求解过程
让我们简要总结一下推导出的 Muon 公式,其中 $\eta$ 是学习率
$$ \mathbf{W}_{} \gets \mathbf{W} - \eta \cdot\mathcal{O}\left(\sqrt{ \frac{m}{n} }\right)\text{NewtonSchulz}(\nabla_{\mathbf{W}}\mathcal{L}), \mathbf{W} \in\mathbb{R}^{m \times n} $$
更新规则
实际上 Muon 的更新规则如下:我们并非是对梯度做正交化,而是对 Nesterov Style 的动量做,然后系数是 $1, \sqrt{ m/n }$ 的最大值
$$ \begin{align} \mathbf{M}_{t} & = \beta \, \mathbf{M}_{t-1} + (1-\beta) \nabla_{\mathbf{W}}\mathcal{L}\\ \mathbf{O}_{t} & = \text{NewtonSchulz}(\beta \,\mathbf{M}_{t} + (1-\beta)\nabla_{\mathbf{W}}\mathcal{L})\\ \mathbf{W}_{t} & = \mathbf{W}_{t-1} - \eta \cdot {\color{#08F}\max \left( 1, \sqrt{ \frac{m}{n} } \right)} \mathbf{O}_{t} \end{align} $$
与谱条件的联系
先联系上述式 $\#1$ 和式 $\#2$:
$$ \begin{align} \|\mathbf{W}\|_{\text{RMS} \to \text{RMS}} & := \max_{\boldsymbol{x} \neq \boldsymbol{0}} \frac{\|\mathbf{W}\boldsymbol{x}\|_{\text{RMS}}}{ \|\boldsymbol{x}\|_{\text{RMS}}} \\ \|\mathbf{W}\|_{\text{RMS} \to \text{RMS}} & = \sqrt{ \frac{n}{m} }\|\mathbf{W}\|_{2} \end{align} $$
那么可以导出:
$$ \|\mathbf{W}\boldsymbol{x}\|_{\text{RMS}} \leq \|\mathbf{W}\|_{\text{RMS}\to \text{RMS}} \|\boldsymbol{x}\|_{\text{RMS}}=\sqrt{ \frac{n}{m} }\|\mathbf{W}\|_{2}\|\boldsymbol{x}\|_{\text{RMS}} \tag{\#6} $$
如果想要控制输出的 RMSNorm,即 $\|\mathbf{W}\boldsymbol{x}\|_{\text{RMS}} = \mathcal{O}(1)$,假设 $\|\boldsymbol{x}\|_{\text{RMS}}=\mathcal{O}(1)$,则:
$$ \sqrt{ \frac{n}{m} }\|\mathbf{W}\|_{2}\|\boldsymbol{x}\|_{\text{RMS}} =\mathcal{O}(1) \implies \|\mathbf{W}\|_{2} =\mathcal{O}\left(\sqrt{ \frac{m}{n} }\right) $$
上面推导 Muon 是约束输出变化量来导出对权重的谱范数进行约束,但严格来说,关于输出变化量的推导是不严谨的,这也是 Muon 和谱条件
https://arxiv.org/abs/2310.17813
(Spectral Condition)的不同之处,因为当权重变了之后,输入也会随之改变,比如第二层的输入其实是第一层的输出,这里推导借鉴了苏老师关于谱条件的介绍
https://kexue.fm/archives/10795
,记 $\boldsymbol{x}_{k}$ 为第 $k$ 层的输出
$$ \begin{align} \Delta \boldsymbol{x}_{k} & = (\boldsymbol{x}_{k-1}+\Delta \boldsymbol{x}_{k-1})(\mathbf{W}_{k}+\Delta \mathbf{W}_{k}) - \boldsymbol{x}_{k-1}\mathbf{W}_{k} \\[5pt] &= \boldsymbol{x}_{k-1}(\Delta \mathbf{W}_{k}) + (\Delta \boldsymbol{x}_{k-1})\mathbf{W}_{k} + (\Delta \boldsymbol{x}_{k-1})(\Delta\mathbf{W}_{k}) \end{align} $$
那么:
$$ \begin{align} \|\Delta \boldsymbol{x}_{k}\|_{\text{RMS}} &= \|\boldsymbol{x}_{k-1}(\Delta \mathbf{W}_{k}) + (\Delta \boldsymbol{x}_{k-1})\mathbf{W}_{k} + (\Delta \boldsymbol{x}_{k-1})(\Delta\mathbf{W}_{k})\|_{\text{RMS}} \\[5pt] &\leq \|\boldsymbol{x}_{k-1}(\Delta \mathbf{W}_{k})\|_{\text{RMS}} + \|(\Delta \boldsymbol{x}_{k-1})\mathbf{W}_{k}\|_{\text{RMS}} + \|(\Delta \boldsymbol{x}_{k-1})(\Delta \mathbf{W}_{k})\|_{\text{RMS}} \\ \end{align} $$
联系式 $\#6$,将三项分开来看,同时沿用假设:$\|\boldsymbol{x}_{k-1}\|_{\text{RMS}}=\mathcal{O}(1), \|\Delta \boldsymbol{x}_{k-1}\|_{\text{RMS}}=\mathcal{O}(1)$
$$ \begin{align} \|\Delta \boldsymbol{x}_{k}\|_{\text{RMS}} & \leq \sqrt{ \frac{n}{m}}\bigg(\|\boldsymbol{x}_{k-1}\|_{\text{RMS}}\|\Delta \mathbf{W}_{k}\|_{2}+\|\Delta \boldsymbol{x}_{k-1}\|_{\text{RMS}}\|\mathbf{W}_{k}\|_{2}+\|\Delta \boldsymbol{x}_{k-1}\|_{\text{RMS}}\|\Delta \mathbf{W}_{k}\|_{2}\bigg) \\[5pt] &\leq \sqrt{ \frac{n}{m} }\bigg(\|\Delta\mathbf{W}_{k}\|_{2}+\|\mathbf{W}_{k}\|_{2}+\|\Delta \mathbf{W}_{k}\|_{2}\bigg) \end{align} $$
若要求 $\|\Delta \boldsymbol{x}_{k}\|_{\text{RMS}} =\mathcal{O}(1)$,则:
$$ \sqrt{ \frac{n}{m}}\bigg(\|\Delta\mathbf{W}_{k}\|_{2}+\underbrace{ \|\mathbf{W}_{k}\|_{2} }_{\mathcal{O}(\sqrt{m/n}) }+\|\Delta \mathbf{W}_{k}\|_{2}\bigg) =\mathcal{O}(1) $$
最后就导出了:
$$ \|\Delta \mathbf{W}_{k}\|_{2} = \mathcal{O}\left(\sqrt{ \frac{m}{n} }\right) $$
从这个角度来看,其实 Muon 是谱条件的子集,因为谱条件不仅要求控制权重的变化量,还要求控制权重本身
直觉解释
为什么要正交化
这里给出两个原因:
Jordan(也就是 Muon 的作者)的博客 https://kellerjordan.github.io/posts/muon/ 中是这样说的:
因为在 Transformer 模型的训练中,梯度矩阵的「条件数」(condition number)通常是非常大的,条件数的一个定义是
$\sigma_{\max} / \sigma_{\min}$,这个值越大,说明梯度矩阵是由少数主要方向主导的,即 low-rank 的结构,然后正交化可以使得那些本来很弱势的方向被重新关注
个人认为「高条件数 -> low-rank」是比较牵强的,比如正常满秩的矩阵,最小的奇异值很小,也会让整体的条件数很大。但梯度矩阵是 low-rank 多半是正确的,那么正交化的确会有让弱势方向的比重增大的优势
然而,如果按照上面的推导就知道,一开始我们是想 bound 住输出变化量的 RMSNorm,进而推导出需要在最速下降的同时控制谱范数
$$ \min \, \langle \nabla_{\mathbf{W}}\mathcal{L},\Delta \mathbf{W}\rangle, \|\Delta \boldsymbol{y}\|_{\text{RMS}} =\mathcal{O}(1) {\color{#08F}\implies} \|\Delta \mathbf{W}\|_{\text{RMS}\to \text{RMS}}=\mathcal{O}(1) {\color{#08F}\implies} \|\Delta \mathbf{W}\|_{2}= \mathcal{O}\left(\sqrt{ \frac{m}{n} }\right) $$
换句话说,Muon 的本质即是「控制谱范数下的最速下降」
为什么控制谱范数
那么问题是,为什么要控制谱范数呢?或者为什么控制谱范数下的最速下降收敛更快,泛化更好呢?直观来说,我们是通过 bound 住输出的变化量 $\|\Delta \boldsymbol{y}\|_{\text{RMS}}$ 来导出需要控制谱范数,如果更新量过大,会使得训练整体就不太稳定,同时控制住之后还可以使得反传的梯度更加健康,总结就是会使得训练过程中前传和反传更加稳定,这也是为什么有些时候 Muon 可以比 Adam 使用更大学习率的原因
花开两朵各表一枝,控制谱范数这个推论还可以由谱条件推出来。谱条件其实为了小模型上的最优参数(比如学习率)可以迁移到更大的模型上,即参数迁移不受模型尺度影响。那么如何做到呢?即让不同尺度的模型具有相同的 training dynamics,通过控制模型每一层的输出和输出变化量的 RMSNorm 来做到。换言之,控制谱范数还可以让不同尺度模型的 training dynamics 相同,从而达到迁移参数的目的
Moonlight
接着来介绍 Kimi 团队在 Muon 上的改进,主要是 weight decay 以及对齐 RMSNorm
Weight Decay
Kimi 团队在进行 scaling 实验时,发现在原始 Muon 的不断更新下,权重的 RMSNorm 会不断变大,可能会超出 bfloat16 的精度,进而有损性能。为了弥补这种情况,加上了权重衰减,即为下式蓝色部分
$$ \mathbf{W}_{t} = \mathbf{W}_{t-1} - \eta(\mathbf{O}_{t} + {\color{#08F}\lambda \mathbf{W}_{t-1}}) $$
加了 weight decay 虽然一开始收敛会慢,但后面就会超过不加 weight decay 的情况;同时,如果不加 weight decay,长时间训练后就会跟 AdamW 很接近

RMSNorm 对齐
将梯度进行奇异值分解: $\nabla_{\mathbf{W}}\mathcal{L}=\mathbf{U\Sigma V^{\top}}$,即 $\mathbf{U}\in\mathbb{R}^{m\times r}, \mathbf{V}\in\mathbb{R}^{n\times r}, \mathbf{\Sigma} \in\mathbb{R}^{r \times r}$,其中 $r=\text{rank}(\nabla_{\mathbf{W}}\mathcal{L})\leq \min(m, n)$
向量的 RMSNorm 计算如下:
$$ \|\boldsymbol{x}\|_{\text{RMS}} = \sqrt{\frac{1}{n}\sum_{i} \boldsymbol{x}_{i}^{2}} $$
那么同理可得矩阵的 RMSNorm 计算:
$$ \|\mathbf{W}\|_{\text{RMS}} = \sqrt{ \frac{1}{mn} \sum_{i}\sum_{j} w_{ij}^{2} } $$
下面推导依然按照先前对「梯度正交化」的角度,首先:
$$ \|\mathbf{O}_{t}\|_{\text{RMS}} = \|\mathbf{UV}^{\top}\|_\text{RMS} = \sqrt{ \frac{1}{mn} \sum_{i=1}^{m} \sum_{j=1}^{n}\sum_{k=1}^{r} u_{ik}^{2}v_{kj}^{2}} $$
由于 $\mathbf{U}, \mathbf{V}$ 都是正交矩阵,所以其行向量和列向量都是「单位向量」,则:
$$ mn \|\mathbf{O}_{t}\|_{\text{RMS}}^{2} = \sum_{i=1}^{m}\sum_{j=1}^{n}\sum_{k=1}^{r} u_{ik}^{2}v_{kj}^{2} = \sum_{k=1}^{r} \left(\sum_{i=1}^{m} u_{ik}^{2}\right)\left(\sum_{j=1}^{n}v_{kj}^{2}\right) = \sum_{k=1}^{r} 1 = r $$
同时因为实际情况下「严格低秩」的概率比较小,所以不妨按满秩来算,即 $r=\min(m,n)$
$$ \|\mathbf{O}_{t}\|_{\text{RMS}} = \sqrt{ \frac{r}{mn} } = \sqrt{ \frac{1}{\max(m, n)} } $$
而实际 LLMs 训练时,不同的权重矩阵 $m,n$ 不同,则导致更新量的 RMSNorm 不均衡,所以可以用一个系数来「归一化更新量的 RMSNorm」,即:
$$ \left\|\sqrt{ \max(m,n) } \cdot \mathbf{O}_{t}\right\|_{\text{RMS}} = 1 $$
同时观察到对于 Adam 来说,其 $\|\mathbf{O}_{t}\|_{\text{RMS}} \in[0.2, 0.4]$,这里为了可以直接迁移之前 Adam 的学习率,就进一步对齐 Adam 更新量的 RMSNorm,即将 Muon 实际上更新量的 RMSNorm 控制在 $0.2$ 左右:
$$ \mathbf{W}_{t} = \mathbf{W}_{t-1} - \eta\left({\color{#08F}0.2\sqrt{ \max(m,n) }}\mathbf{O}_{t}+\lambda \mathbf{W}_{t-1}\right) $$
对比一下 Muon 的系数:
$$ \mathbf{W}_{t} = \mathbf{W}_{t-1} - \eta\left( {\color{#08F}\max\left( 1,\sqrt{ \frac{m}{n} }\right)} \mathbf{O}_{t} + \lambda \mathbf{W}_{t-1}\right ) $$
实现
接下来到了喜闻乐见的上代码环节,具体会实现原始的 Muon 以及 Kimi 在 Muon 上的改进
Newton Schulz 迭代
Newton Schulz 的实现主要参考官方的源代码
https://github.com/KellerJordan/Muon/blob/master/muon.py
,记 Frobenius Norm $\|\mathbf{W}\|_{\text{F}}$,其定义如下:
$$ \|\mathbf{W}\|_{\text{F}} = \sqrt{ \sum_{i}\sum_{j} w_{ij}^{2}} $$
接着我们来证明「Frobenius 归一化可以使得矩阵的奇异值缩放到 $[0, 1]$ 之间」,Frobenius Norm 满足下式:
$$ \|\mathbf{W}\boldsymbol{x}\|_{\text{F}} \leq \|\mathbf{W}\|_{\text{F}}\|\boldsymbol{x}\|_{\text{F}} $$
联想一下,对于向量来说的 L2 norm,不就是 Frobenius Norm 的一种形式嘛:
$$ \forall \boldsymbol{x}, \frac{\|\mathbf{W}\boldsymbol{x}\|_{2}}{\|\boldsymbol{x}\|_{2}} = \frac{\|\mathbf{W}\boldsymbol{x}\|_{\text{F}}}{\|\boldsymbol{x}\|_{\text{F}}} \leq \frac{\|\mathbf{W}\|_{\text{F}}\|\boldsymbol{x}\|_{\text{F}}}{\|\boldsymbol{x}\|_{\text{F}}} = \|\mathbf{W}\|_{\text{F}} $$
联系上面我们推导的结果:
$$ \max_{\boldsymbol{x}\neq\boldsymbol{0}} \frac{\|\mathbf{A}\boldsymbol{x}\|_{2}}{\|\boldsymbol{x}\|_{2}} = \|\mathbf{A}\|_{2} \leq \|\mathbf{A}\|_{\text{F}} $$
也就是说「Frobenius Norm 大于或等于 Spectral Norm」,那么 Spectral Norm 代表的是最大的奇异值,这就可以导出 Frobenius Norm 归一化后的矩阵的奇异值在 $[0,1]$ 之间
Newton Schulz 实现
def newton_schulz5(
gradient: Tensor,
steps: int = 5,
coefficients: list[float] = [3.4445, -4.7750, 2.0315],
eps: float = 1e-7,
):
"""
1. 用 Newton Schulz 计算矩阵的零次幂, 只负责二维矩阵, 系数是 Muon 官方搜出
2. 给定 gradient SVD = USV^T, 尽管初衷是通过 NS 来让 \Sigma 变成 I,
从而完成对梯度的正交化, 即 UV^T, 但实际上是 US'V^T, S'_ii \in [1-e, 1+e],
并且不影响实际效果
"""
assert gradient.ndim >= 2
dim1, dim2 = gradient.size(-2), gradient.size(-1)
gradient = gradient.bfloat16()
# 运算时会大量涉及 g @ g^T, 所以形状是 (dim1, dim1)
# 但如果 dim1 过大,运算效率和内存开销都不友好
# 所以可以转置,最后返回前转回来即可
if dim1 > dim2:
gradient = gradient.mT
# 进行 Frobenius Norm 以确保奇异值在 [0, 1]
x = gradient / (gradient.norm() + eps)
a, b, c = coefficients
for _ in range(steps):
xx_T = x @ x.mT
xx_Tx = xx_T @ x
x = a * x + b * xx_Tx + c * (xx_T @ xx_Tx)
if dim1 > dim2:
x = x.mT
return x
下图是 $y=ax + bx^{3}+cx^{5}$ 以及 $y=1$(红线),观察发现等于 $1$ 的情况不多
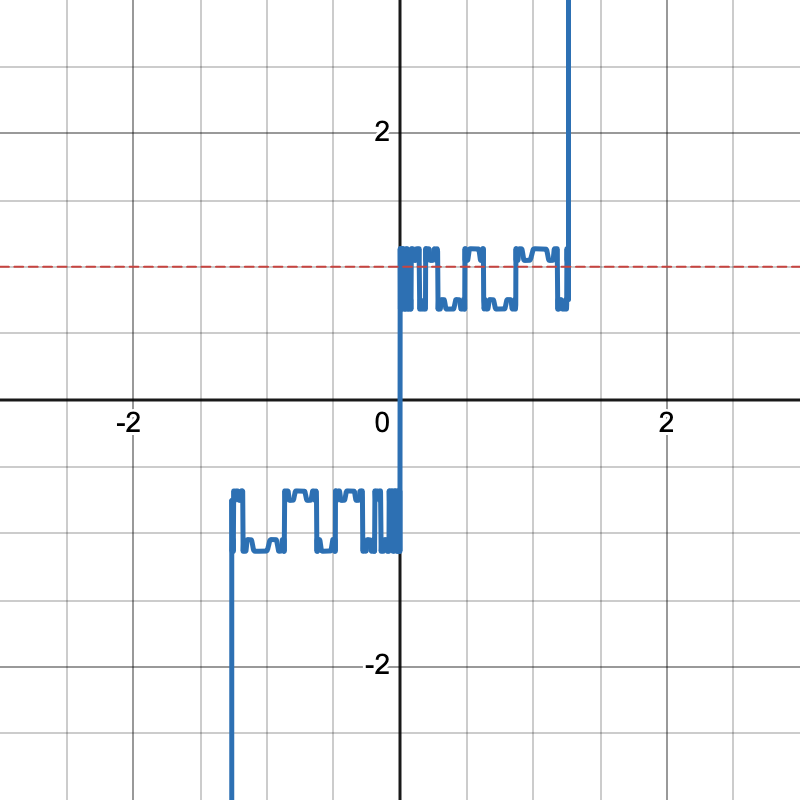
换句话说,似乎假设并不成立了
$$ \begin{align} \text{Theory: } \nabla_{\mathbf{W}}\mathcal{L} & = \mathbf{U\Sigma V^{\top}} \mapsto \mathbf{UV^{\top}} \\ \text{Empricial: } \nabla_{\mathbf{W}} \mathcal{L} & = \mathbf{U\Sigma V^{\top}} \mapsto \mathbf{U{\color{#08F}\Sigma'}V^{\top}}, \Sigma_{ii}' \in [0.6, 1.2] \end{align} $$
真实实验结果是我们需要确保在 $[0,1]$ 内收敛到 $[1-\epsilon, 1+\epsilon]$ 即可,按照 Jordan 的博客, $\epsilon$ 可以大到 $0.3$ 而不影响性能,并不需要严格等于 $1$
还有一个问题,为什么使用 Newton-Schulz 来进行正交化呢?因为正交化还可以用其他方法:
- 不使用 SVD 的原因是因为太慢了
- 不使用 Coupled Newton Iteration 是因为在 bfloat16 上不稳定,至少得需要 float32 才行
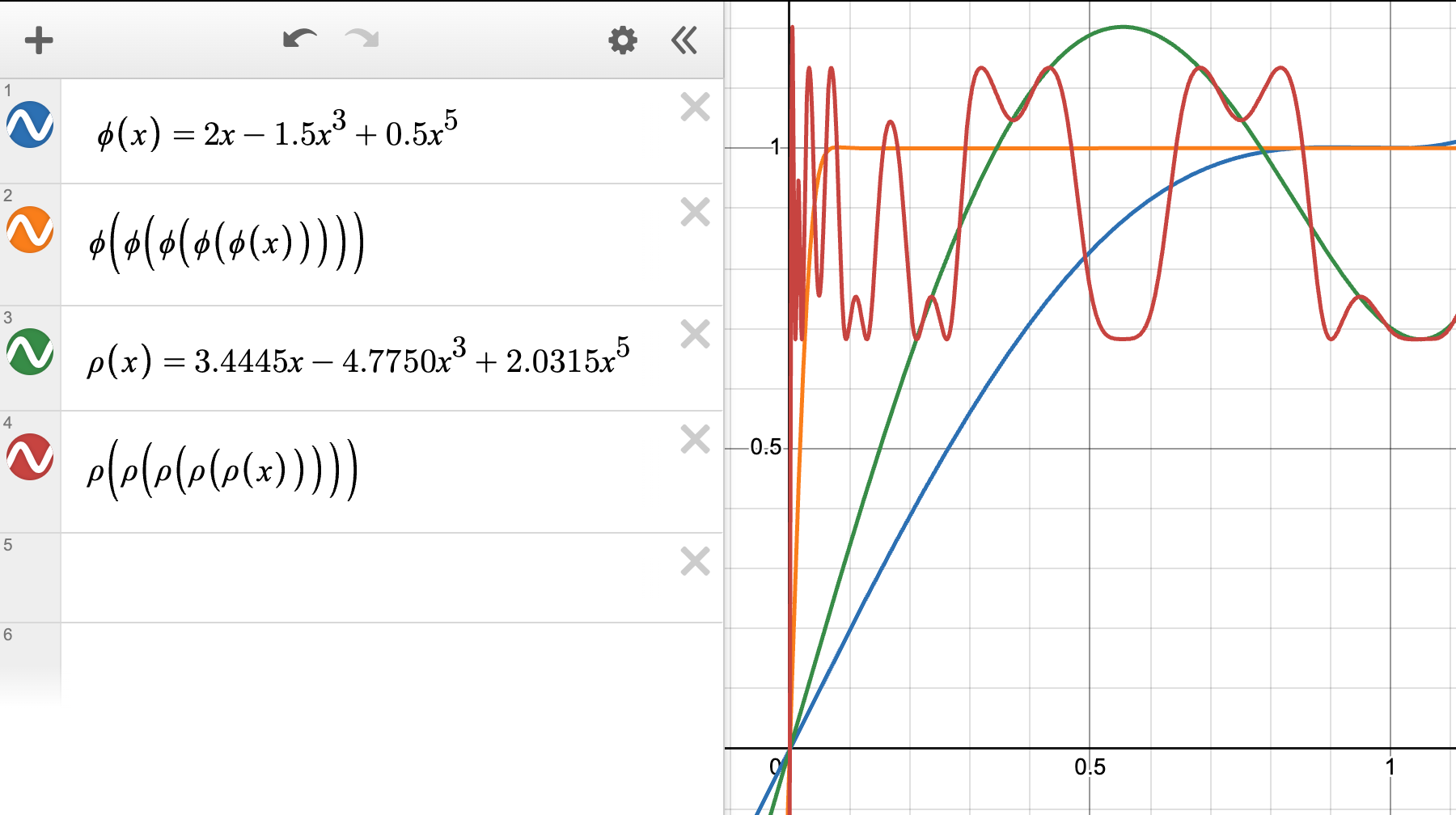
再简单说说如何来微调这些系数,下图是两种系数的对比(取自 Jordan 的博客):
主要就是 $\phi'(0)$ 的值,或者说 $0$ 处以及附近点的斜率,这个决定了初始的收敛速度,大些是更好的
更新
接着来实现 Muon 的更新规则,默认加上了 weight decay,以及通过判断 rms_match 是否为 None 来决定使用 Kimi 的 rms match 还是官方默认的 scale 系数
Muon 更新代码
class Muon(torch.optim.Optimizer):
... # 先省略其他部分
@torch.no_grad()
def step_muon(self, param_groups):
def update_momentum():
momentum.lerp_(grad, 1 - beta)
momentum_ns = beta * momentum + (1 - beta) * grad if nesterov else momentum
return momentum_ns
def update():
p.mul_(1 - lr * weight_decay)
if rms_match is not None: # 使用 Kimi 提出的 scale
scale = rms_match * math.sqrt(max(p.shape[-2:]))
else: # original scale by KellerJordan
scale = max(1, p.size(-2) / p.size(-1))**0.5
p.add_(delta, alpha=-lr * scale)
for group in param_groups:
params = group['params']
lr = group['lr']
weight_decay = group['weight_decay']
beta = group['beta']
nesterov = group['nesterov']
ns_steps = group['ns_steps']
rms_match = group['rms_match']
for p in params:
grad = p.grad
state = self.state[p]
if 'momentum' not in state:
state['momentum'] = torch.zeros_like(
grad, memory_format=torch.preserve_format
)
momentum = state['momentum']
momentum_ns = update_momentum()
if momentum_ns.ndim == 4: # 拉伸 conv filter 参数
momentum_ns = momentum_ns.view(momentum_ns.size(0), -1)
delta = self.newton_schulz5(momentum_ns, ns_steps)
update()
def newton_schulz5(
self,
gradient: Tensor,
steps: int = 5,
coefficients: list[float] = [3.4445, -4.7750, 2.0315],
eps: float = 1e-7,
):
"""
1. 用 Newton Schulz 计算矩阵的零次幂, 只负责二维矩阵, 系数是 Muon 官方搜出
2. 给定 gradient SVD = USV^T, 尽管初衷是通过 NS 来让 \Sigma 变成 I,
从而完成对梯度的正交化, 即 UV^T, 但实际上是 US'V^T, S'_ii \in [1-e, 1+e],
并且不影响实际效果
"""
assert gradient.ndim >= 2
dim1, dim2 = gradient.size(-2), gradient.size(-1)
gradient = gradient.bfloat16()
# 运算时会大量涉及 g @ g^T, 所以形状是 (dim1, dim1)
# 但如果 dim1 过大,运算效率和内存开销都不友好
# 所以可以转置,最后返回前转回来即可
if dim1 > dim2:
gradient = gradient.mT
# 进行 Frobenius Norm 以确保奇异值在 [0, 1]
x = gradient / (gradient.norm() + eps)
a, b, c = coefficients
for _ in range(steps):
xx_T = x @ x.mT
xx_Tx = xx_T @ x
x = a * x + b * xx_Tx + c * (xx_T @ xx_Tx)
if dim1 > dim2:
x = x.mT
return x
与 Adam 一道
使用时,对于非矩阵参数(比如 Layer Norm 的 gamma 系数)以及 embed, lm_head 的部分需要使用 Adam 来进行优化,所以还需要加入拆分参数以及 Adam 的使用,这里也列出 Adam 的更新规则来便于读者对照阅读代码:
$$ \begin{align} \boldsymbol{m}_{t} & = \beta_{1}\boldsymbol{m}_{t-1} + (1-\beta_{1})\nabla_{\mathbf{W}}\mathcal{L} \\ \boldsymbol{v}_{t} & = \beta_{2}\boldsymbol{v}_{t-1} + (1-\beta_{2})\nabla_{\mathbf{W}}^{2}\mathcal{L} \\ \boldsymbol{\hat{m}}_{t} & = \frac{\boldsymbol{m}_{t}}{1- \beta_{1}^{t}}, \boldsymbol{\hat{v}}_{t} = \frac{\boldsymbol{v}_{t}}{1-\beta_{2}^{t}} \\ \mathbf{W}_{t} & = \mathbf{W}_{t-1} - \eta\left( \frac{\boldsymbol{\hat{m}}_{t}}{\sqrt{ \boldsymbol{\hat{v}}_{t} }+\epsilon} + \lambda \mathbf{W}_{t-1} \right) \end{align} $$
还有一条实践的 tip,如果是用在 Transformer 中的 Q,K,V 上,最好是单独的权重,而不是整体一个大的权重,然后再 split 出 Q,K,V
Muon 整体实现
class Muon(torch.optim.Optimizer):
def __init__(
self,
lr: float, # 仅占位符
params: Iterator[Tuple[str, Parameter]],
weight_decay: float = 0.1,
beta: float = 0.95,
nesterov: bool = True,
ns_steps: int = 5,
rms_match: float = 0.2,
adam_betas: list[float] = [0.9, 0.999],
adam_eps: float = 1e-8,
):
param_groups = self.split_params(params)
other_defaults = dict(betas=adam_betas, eps=adam_eps)
param_groups = [
dict(
params=param_groups['hidden_matrix_params'], # Muon 去优化的参数
weight_decay=weight_decay,
beta=beta,
nesterov=nesterov,
ns_steps=ns_steps,
rms_match=rms_match
),
dict(
params=param_groups['non_matrix_params'],
weight_decay=0., # 默认非矩阵参数不加 weight decay
**other_defaults
),
dict(
params=param_groups['embed_lm_head_matrix_params'],
weight_decay=weight_decay,
**other_defaults,
)
]
super().__init__(param_groups, {})
def step(self):
muon_param_groups = [group for group in self.param_groups if 'ns_steps' in group]
other_param_groups = [
group for group in self.param_groups if 'ns_steps' not in group
]
self.step_muon(muon_param_groups)
self.step_adamw(other_param_groups)
@torch.no_grad()
def step_muon(self, param_groups):
...
@torch.no_grad()
def step_adamw(self, param_groups):
def update_momentum():
momentum1.lerp_(grad, 1 - beta1)
momentum2.lerp_(grad.square(), 1 - beta2)
def update():
bias_correction1 = 1 - beta1**step
bias_correction2 = 1 - beta2**step
scale = bias_correction1 / bias_correction2**0.5
delta = momentum1 / (momentum2.sqrt() + eps)
p.mul_(1 - lr * weight_decay)
p.add_(delta, alpha=-lr / scale)
for group in param_groups:
params = group['params']
lr = group['lr']
weight_decay = group['weight_decay']
beta1, beta2 = group['betas']
eps = group['eps']
for p in params:
grad = p.grad
state = self.state[p]
if 'step' not in state:
state['step'] = 0
state['momentum1'] = torch.zeros_like(
grad, memory_format=torch.preserve_format
)
state['momentum2'] = torch.zeros_like(
grad, memory_format=torch.preserve_format
)
momentum1 = state['momentum1']
momentum2 = state['momentum2']
state['step'] += 1
step = state['step']
update_momentum()
update()
def split_params(self, params: Iterator[Tuple[str, Parameter]]):
# params: model.named_parameters()
# Muon 只负责优化除了 embed, lm_head 之外的「矩阵」参数
param_dict = {pn: p for pn, p in params if p.requires_grad}
non_matrix_params = [p for p in param_dict.values() if p.ndim < 2]
embed_lm_head_matrix_params = [
p for pn, p in param_dict.items()
if p.dim() >= 2 and ('embed' in pn or 'lm_head' in pn)
]
hidden_matrix_params = [
p for pn, p in param_dict.items() if p.ndim >= 2 and 'layers' in pn
]
return dict(
non_matrix_params=non_matrix_params,
embed_lm_head_matrix_params=embed_lm_head_matrix_params,
hidden_matrix_params=hidden_matrix_params
)
def newton_schulz5(
self,
gradient: Tensor,
steps: int = 5,
coefficients: list[float] = [3.4445, -4.7750, 2.0315],
eps: float = 1e-7,
):
...
实验
setting
| 设定 | 数值 |
|---|---|
$\#$params | 0.6B |
$\#$ train tokens | 58B |
$\#$ eval tokens | 0.2B |
| lr | 8e-4 |
| weight decay | 0.1 |
| seq length | 8192 |
| global batch | 384 |
| LR schedule | linear warm (0.01) cosine decay (1.) |
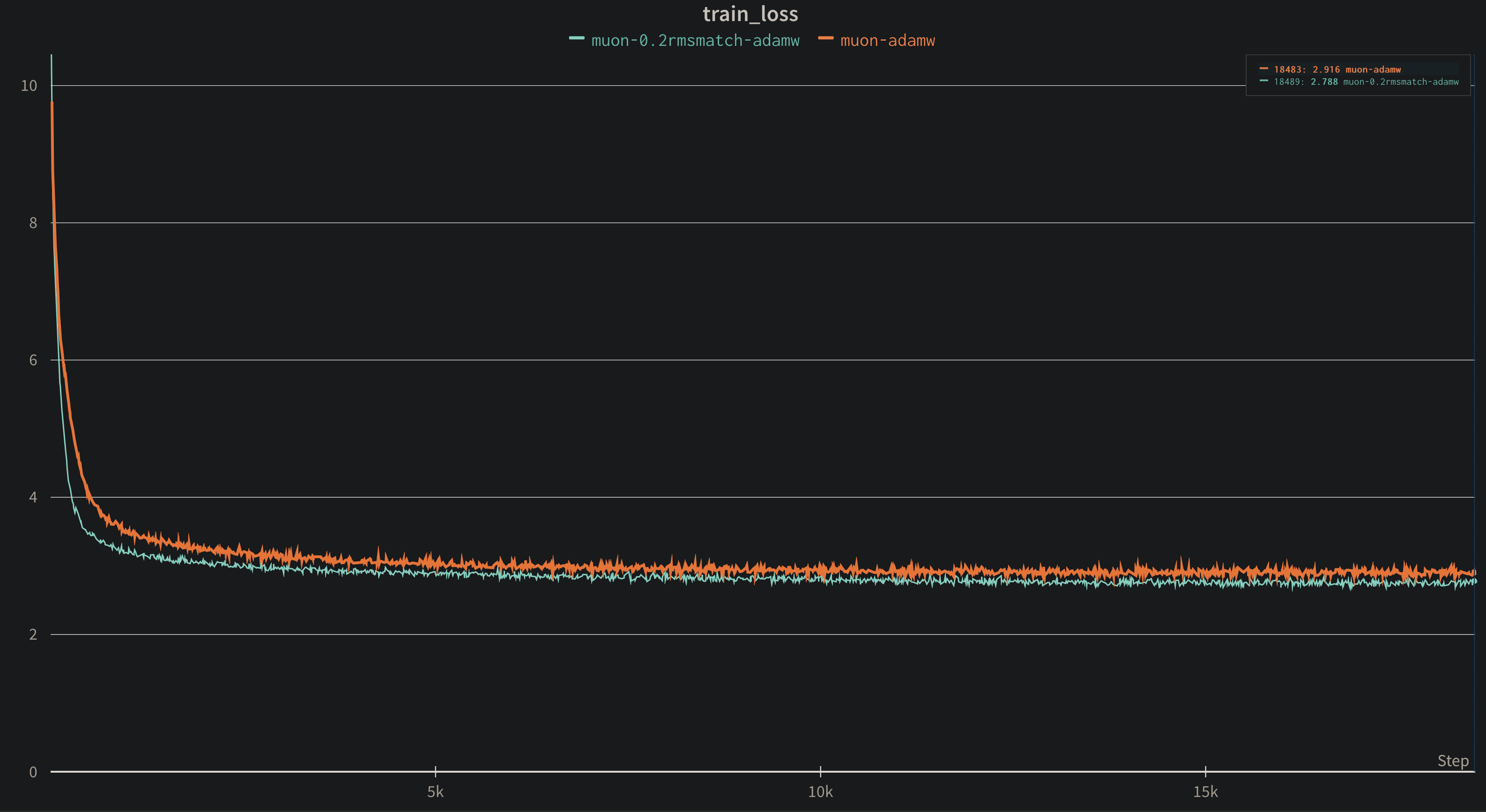
不同的 scale 系数
首先是对照原始 Muon 和 Kimi Muon 的系数,这里偷懒就不单独为原始的 Muon 像 speedrun 那样为 Adam 和 Muon 调制不同的学习率,统一用一个学习率,可以发现无论是训练还是 eval,Kimi 的系数都会更好
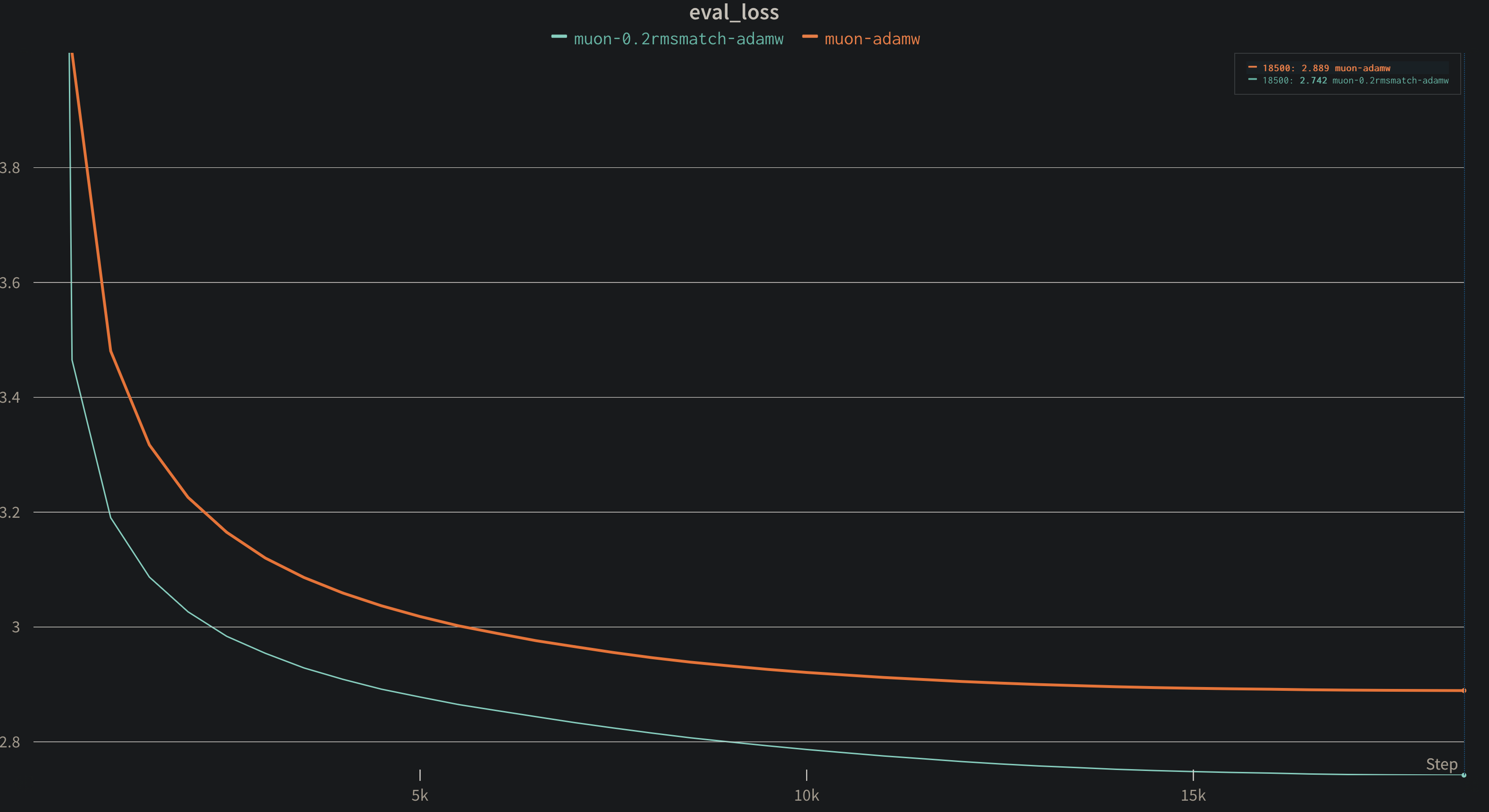
Kimi Muon VS AdamW
接着我们来与 AdamW 对比,可以发现是 Kimi Muon 收敛更快
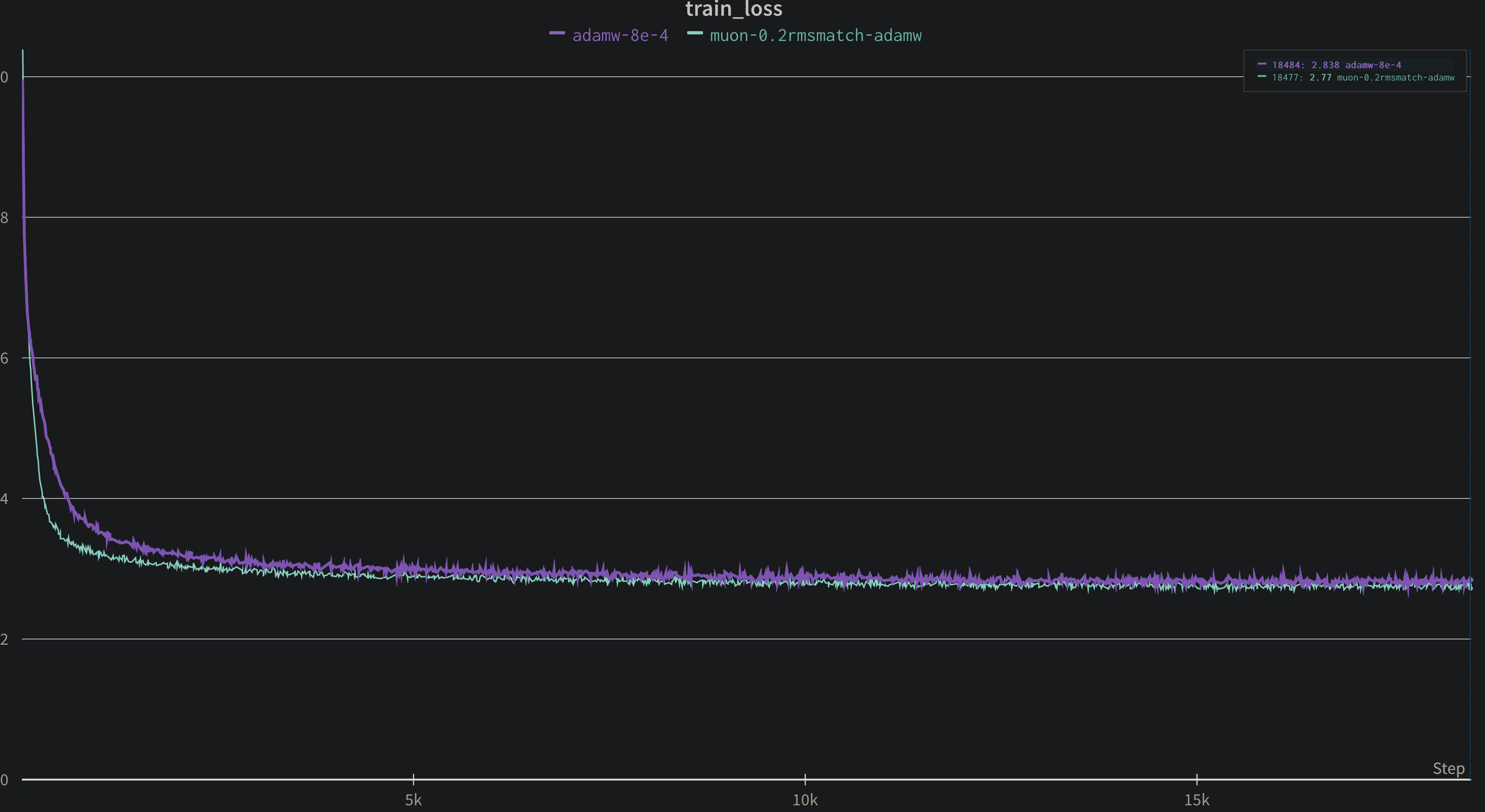
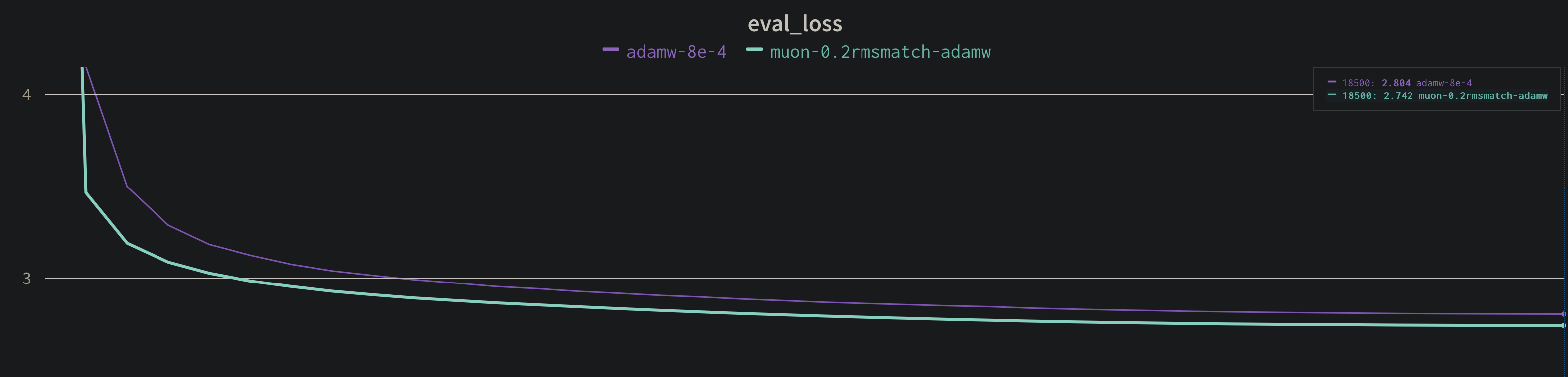
FLOPs 分析
我们来分析一下 FLOPs(浮点数运行次数),对于一个 $\mathbf{A} \in\mathbb{R}^{m\times n},\mathbf{B}\in\mathbb{R}^{n\times p}$,两者相乘的 FLOPs 是 $mp(2n-1)=2mnp-mp$,$mp$ 是新矩阵的元素个数,然后每个新矩阵的元素需要经过 $n$ 次乘法和 $n-1$ 次加法
介绍完基本概念,来先分析一下 NS 迭代的 FLOPs,主要的计算量在如下代码处:
for _ in range(steps):
xx_T = x @ x.mT # 1. m x n, n x m => m x m
xx_Tx = xx_T @ x # 2. m x m, m x n => m x n
# 3. xx_T @ xx_Tx: m x m, m x n => m x n
x = a * x + b * xx_Tx + c * (xx_T @ xx_Tx) # 4
对于 1 的操作,FLOPs 为 $m^{2}(2n-1)=2m^{2}n-m^{2}$;对于 2 的操作,FLOPs 为 $mn(2m-1)=2m^{2}n-mn$;对于 3 的操作,FLOPS 为 $mn(2m-1) = 2m^{2}n-mn$,然后需要将其进行相加:
$$ \begin{align} \underbrace{ 2m^{2}n-m^{2} }_{ \mathbf{XX^{\top}} }+\underbrace{ 2m^{2}n-mn }_{ \mathbf{XX^{\top}X} } + \underbrace{ mn }_{ a\mathbf{X} } +\underbrace{ mn }_{ b\mathbf{XX^{\top}X} } + \underbrace{ mn }_{ c \times \dots } + \underbrace{ 2m^{2}n-mn }_{ \mathbf{XX^{\top}XX^{\top}X} } + \underbrace{ 2mn }_{ \text{ 两次加法} } \\ = 6m^{2}n-m^{2}+3mn \approx 6m^{2}n \end{align} $$
然后我们运行 $T$ 步 NS 迭代,即为 $6Tm^{2}n$
对于一个线性层来说,我们对其进行前向和反向的计算的 FLOPs 为多少?这里省略对于偏置的计算,因为不是主要计算量,记输入矩阵 $\mathbf{X} \in \mathbb{R}^{B\times m}$
$$ \begin{align} &\text{Forward: } \mathbf{Y} = \mathbf{XW}: B\times m, m\times n= B\times n\implies Bn(2m-1) \approx 2Bmn \\ &\text{Backward 1: } \frac{\text{d}\mathcal{L}}{\text{d}\mathbf{X}} = \frac{\text{d}\mathcal{L}}{\text{d}\mathbf{Y}}\mathbf{W^{\top}}: B\times n, n \times m \implies Bm(2n-1)\approx 2Bmn \\ &\text{Backward 2: } \frac{\text{d}\mathcal{L}}{\text{d}\mathbf{W}} = \mathbf{X}^{\top}\frac{\text{d}\mathcal{L}}{\text{d}\mathbf{Y}}: m \times B, B\times n\implies mn(2B-1)\approx 2Bmn \end{align} $$
所以整个加起来即为 $6Bmn$,这里计算输入的梯度是因为在网络中,当前的输入其实就是前一层的输出,计算当前输入的梯度是为了 back-propogation 的时候便于计算
那么使用 Muon 时额外带来的开销是:
$$ \frac{6Tm^{2}n}{6Bmn} = \frac{Tm}{B} $$
当 $T=5$ 时,对于 nanoGPT 以及 Llama 405B 而言,额外的开销并不算很大:
$$ \begin{align} &\text{nanoGPT: } 5 \times \frac{768}{524288} = 0.7\% \\ &\text{Llama 405B: } 5 \times \frac{16384}{16\times10^{6}} = 0.5\% \end{align} $$